Cuando estudiamos en Geometría los cuerpos de revolución solemos quedarnos con las fórmulas de las áreas y los volúmenes correspondientes...Pero consideramos interesante entender de dónde viene el nombre...
¿Qué entendemos por revolución?
Si pensamos en revolución, lo primero que se nos viene a la cabeza es la Revolución Francesa. Pero no siempre la palabra revolución tuvo esta connotación político/social.
Revolución viene del verbo latín revolvere que significa volver a girar que con el uso derivó en el sustantivo revolutio que sería la palabra que hoy entendemos como revolución. En la astronomía medieval la palabra revolución se asoció el término revoluciones a las vueltas que daba un cuerpo celestial, llegando a ser el título de la obra de Copérnico: De revolutionibus orbium coelestium que traducido sería Sobre el movimiento de los cuerpos celestes.
El trabajo de Copérnico tuvo tanto impacto, que desde entonces cualquier suceso que supone un cambio trascendental se le asocia el nombre de reolución.
Y ahora que ya sabemos el porqué del nombre...debemos recordar que:
- Un cilindro es el resultado de hacer revolucionar un rectángulo sobre uno de sus lado.
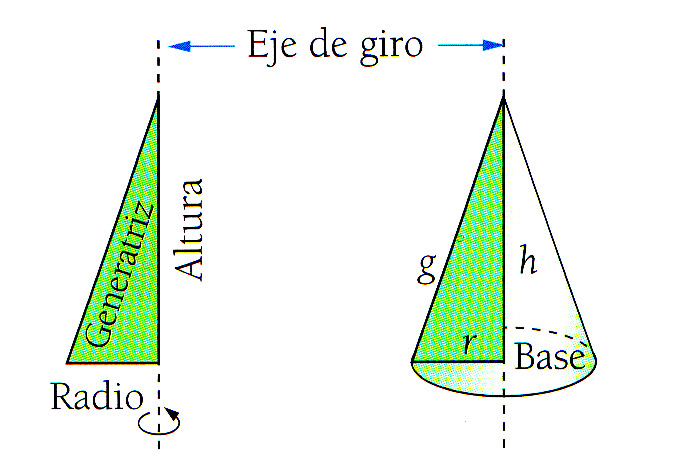
- Un cono es el resultado de hacer revolucionar un triángulo rectángulo sobre uno de sus catetos.
- Una esfera es el resultado de hacer revolucionar un círculo sobre cualquiera de sus diámetros.
La geometría fue descubierta en Egipto, teniendo su origen en la medición de áreas ya que esta era una necesidad para los egipcios debido a que la crecida anual del río Nilo inundaba los campos. Esto generaba varios problemas como, por ejemplo, que debido a que la tierra se distribuía entre los egipcios en terrenos rectangulares iguales, por los que pagaban un impuesto anual, cuando el río inundaba parte de su tierra, el dueño pedía una deducción proporcional en el impuesto, y los agrimensores de aquel tiempo tenían que certificar que tal fracción de tierra había sido inundada. El otro problema surgía cuando el agua volvía a su cauce, ya que la crecida se llevaba las señales que indicaban los límites del terreno de cada egipcio, luego era necesario calcular el área de cada parcela agrícola para restablecer sus límites. Además de eso, el cálculo del área aporta información respecto a cómo podemos sembrar dicho campo o qué cantidad de fertilizante utilizar.
